triadaelectric.blogg.se - Calculate standard error for sampling distribution

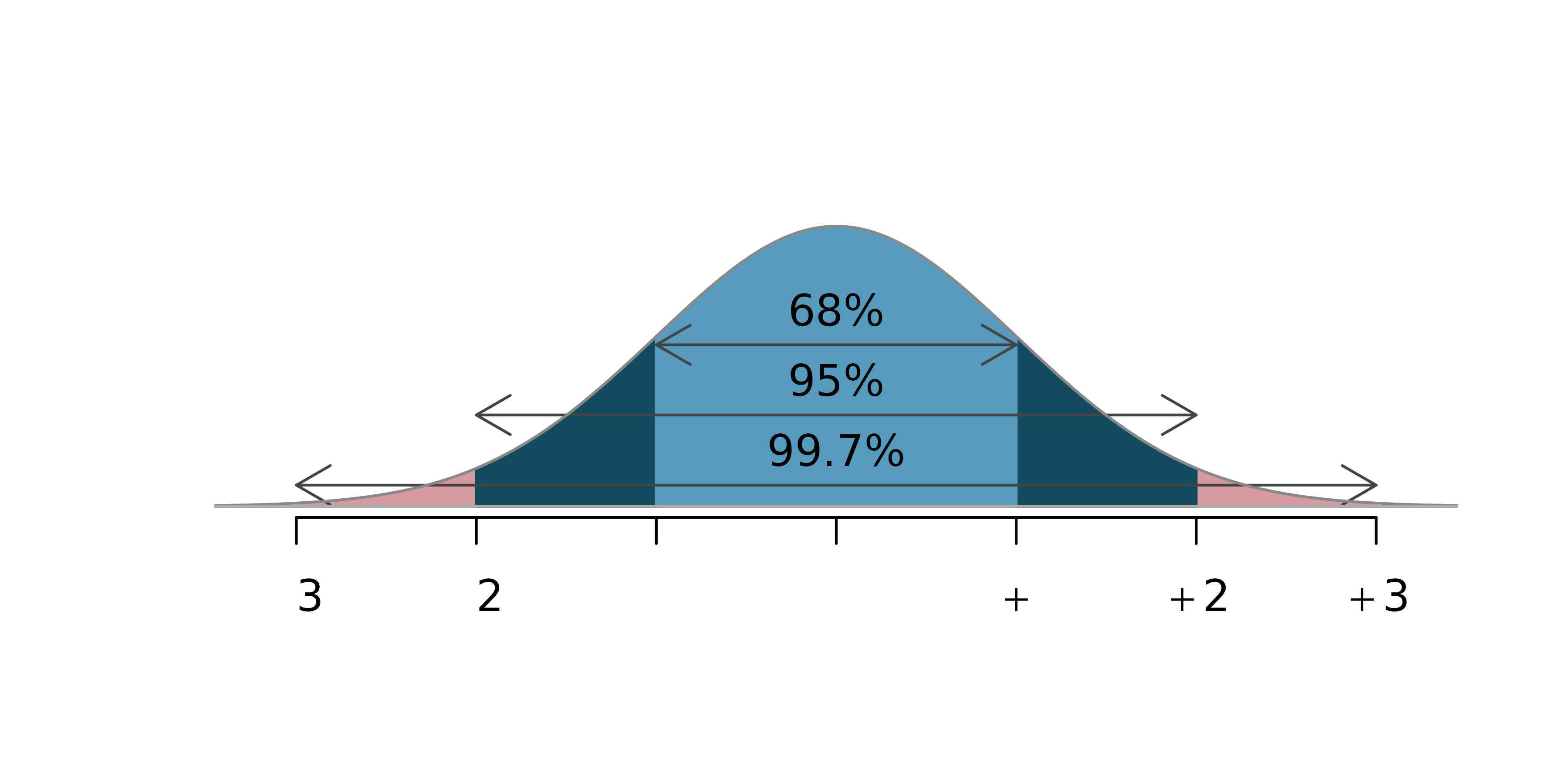
The 100 slips of paper are then put back into the large container with the other 1900 (a process called with sampling with replacement) and the container shuffled and mixed. You then draw out a sample of 100 slips of paper, calculate the mean for this sample of 100, record that mean on a piece of paper, and place it in a second smaller container. This situation can be demonstrated or simulated by recording the 2000 values on separate slips of paper and placing them in a large container.

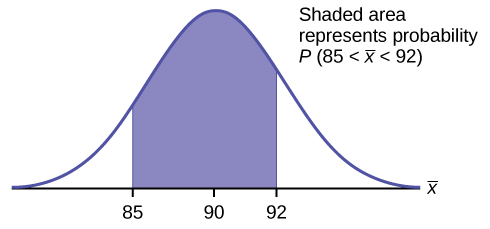
How close would you be if you only analyzed 100 specimens? Assume that the mean (µ) for the whole population is 100 mg/dl.

This would be a lot of work, but the whole population could be tested and the true mean calculated, which would then be represented by the Greek symbol mu (µ). Blood specimens could be drawn from all 2000 patients and analyzed for glucose, for example.

A simulated experimentĬonsider the situation where there are 2000 patients available and you want to estimate the mean for that population. The values calculated from the entire population are called parameters (mu for the mean, sigma for the standard deviation), whereas the values calculated from a smaller sample are called statistics (Xbar for the mean, SD for the standard deviation). In estimating the central location of a group of test results, one could attempt to measure the entire population or to estimate the population parameters from a smaller sample. The calculation of a mean is linked to the central location or correctness of a laboratory test or method (accuracy, inaccuracy, bias, systematic error, trueness) and the calculation of an SD is often related to the dispersion or distribution of results (precision, imprecision, random error, uncertainty). In either case, individual control values should exceed the calculated control limits (expected range of values) and signal that something is wrong with the method. Changes in the method performance may cause the mean to shift the range of expected values, or cause the SD to expand the range of expected values. A common application of these statistics is the calculation of control limits to establish the range of values expected when the performance of the laboratory method is stable. The previous lesson described the calculation of the mean, SD, and CV and illustrated how these statistics can be used to describe the distribution of measurements expected from a laboratory method.

Why are the standard error and the sampling distribution of the mean important?.

Standard deviation of means, standard error of the mean.

Calculation of the mean of the means of samples (or standard error of the mean).

Calculation of the mean of a sample (and related statistical terminology).

EdD Assistant ProfessorĬlinical Laboratory Science Program University of Louisville Zady, Ph.D., talks about the means of means and other important statistical calculations. When you compare monthly QC data or perform initial method validation experiments, you do a lot of mean comparison. The standard error of the mean is the expected value of the standard deviation of means of several samples, this is estimated from a single sample as:Ĭopyright © 2000-2021 StatsDirect Limited, all rights reserved. If a variable y is a linear (y = a + bx) transformation of x then the variance of y is b² times the variance of x and the standard deviation of y is b times the variance of x. When distributions are approximately normal, SD is a better measure of spread because it is less susceptible to sampling fluctuation than (semi-)interquartile range. For any symmetrical (not skewed) distribution, half of its values will lie one semi-interquartile range either side of the median, i.e. Semi-interquartile range is half of the difference between the 25th and 75th centiles. Interquartile range is the difference between the 25th and 75th centiles. This is not the case when there are extreme values in a distribution or when the distribution is skewed, in these situations interquartile range or semi-interquartile are preferred measures of spread. SD is the best measure of spread of an approximately normal distribution. All three terms mean the extent to which values in a distribution differ from one another. The spread of a distribution is also referred to as dispersion and variability. The unbiased estimate of population variance calculated from a sample is: Variance is usually estimated from a sample drawn from a population. SD is calculated as the square root of the variance (the average squared deviation from the mean). The standard deviation of the mean (SD) is the most commonly used measure of the spread of values in a distribution.